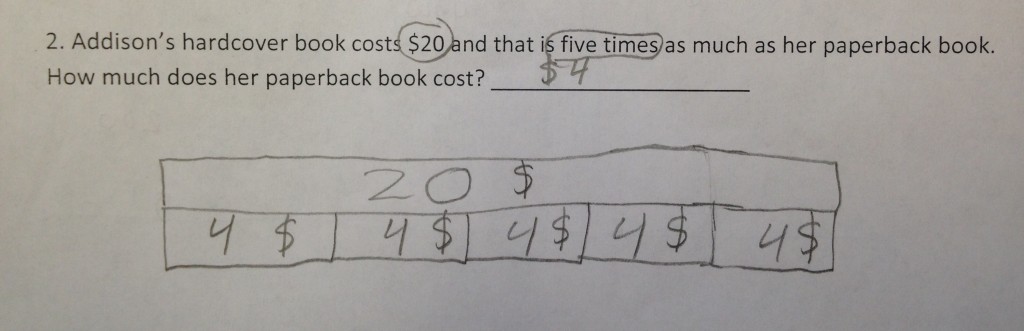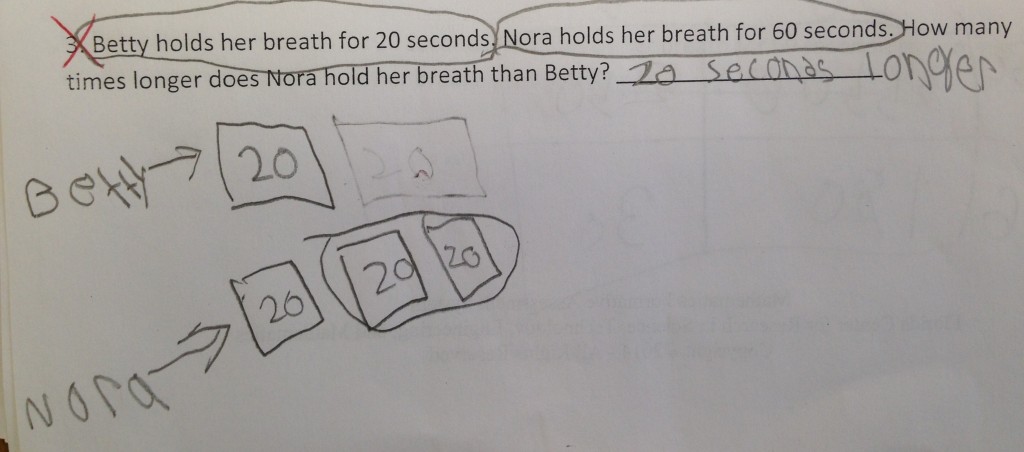WHY AND Z MATH – Page 2 – QUESTIONS AND CONVERSATIONS ABOUT TEACHING MATHEMATICS

Multiplicative Comparison Lesson Study – Part 2

One aspect of lesson study that I really appreciate is how the learning lingers well beyond the end of the study. During this cycle our team learned a lot about using representations to support students’ understanding of multiplicative comparison word problems. I knew though, that as I milled our work over in my mind, there would be more learning; nuggets that were currently hidden, but would be unearthed as I continued to reflect on the work.

We implemented our lesson on multiplicative comparison (MAFS.4.OA.1.2 or CC.4.OA.2). If you’re curious about the general structure of the lesson and the research we consulted while writing it you can check out my first post here.

The First Implementation

In the first class that we implemented the lesson, students noticed a lot of things about the bar model (see figure 1) in the warm-up, but didn’t compare the lengths right away. They noticed the colors, the pattern, and how there were six sections total. We were deliberate about introducing a representation that we thought would be useful to students (NCTM, 2011), but there was some guidance needed to get to where students were using the visual models to compare quantities. Also, we didn’t see a lot of students adopt the visual model to support their sense making and explanations during the main task of the lesson.

figure 1

Debrief and Revision

Our debrief and revision time was quick due to a substitute not showing up. During the debrief we all shared what we had collected in regards to students using the visual model and dialogue that would illustrate student understanding. We all agreed that there had been little transfer in regards to students using the visual models. We decided to make the warm-up task a little more explicit in the line of questioning around the visual model and what we wanted them to notice. Rather than ask them, “What do you notice? What do you wonder?,” we asked students, “What do you notice about the top row and bottom row?” We were hoping that this would better focus students’ attention on the different lengths.

The Second Implementation and Debrief

During the second implemenation we went forward with this more explicit warm-up. Students moved to comparing quantities with the bar model, but still didn’t take the bar model and run with it during the main task. We used a planning period to debrief the second implementation of the lesson and determined that the bar model was a good model, but students just needed more time with it. This was challenging for our team because we knew that this was a single lesson, but really wanted to see evidence that students were moving forward in their thinking. We acknowledged that students needed more time representing these types of problems and decided to spend the rest of the week and the next on the same standard during the intervention block. This gave us about 75 extra minutes of instructional time to utilize what we had learned.

The Follow-Up

Following the lesson study there was some conversation between my interventionist and I about how to best move students forward with the additional instructional time we had. We decided to encourage students to use snap cubes or base ten blocks to model and make sense of the multiplicative comparison situations. We thought that going back to a concrete representation could support student understanding of these problems. In following up with this work during the intervention block one of the tasks we used was:

Jake had 18 toy cars. This was three times as much as his little brother. How many toy cars did his little brother have.

We encouraged students to model the problem with manipulatives or drawings, temporarily abandoning the focus on equations to emphasize sense making. There was something about being able to physically iterate the bar of 6 along the bar of 18 that really supported students seeing the relationship between the two amounts. When I asked students “Is that one (the bar of 18) three times bigger than that one (the bar of 6)?” students moved the smaller bar along the bigger bar to prove that it was. Also, we saw students’ comfort level with explanation of the relationship skyrocket. After seeing the response of students to using manipulatives, one of our team members exclaimed, “We totally should have written that into our research lesson.” Our team hadn’t considered that 4th grade students would need this type of experience with manipulatives. It makes sense though, as this is their first experience using multiplication to compare. Also, we saw students naturally begin moving toward drawings rather than continue using the blocks. The move to encourage students to go back to the concrete wasn’t a new idea, but it was exciting to see students respond so positively to a strategy.

Last week we reassessed this standard with an assessment that included all three types of multiplicative comparison problems (result unknown, measurement division, and partitive division) and saw a mixed bag in regards to the raw scores. While many students showed significant improvement in their raw scores, others did not. Often, the students’ raw scores didn’t reflect the learning that had taken place. A spattering of what we saw is illustrated below with some samples of student work. Over the two weeks we saw an increase in students using visual models to help them make sense of problems (see figure 2).

figure 2

There were instances where students were able to accurately represent the problem, but made a computational error (see figure 3). Here it looks like the student miscounted and forgot to count one of the 7’s.

figure 3

In other instances, the student used an accurate representation, but wasn’t able to “find” the solution in their model. (see figure 4)

figure 4

I think both pieces of student work that were incorrect illustrate how a student can bring a lot of understanding to a situation, even on a missed item. I can see these students arriving at a correct solution with a little discussion and feedback. Also, I like these last two samples because it shows how students began utilizing labels to communicate what the different parts of their drawings represented.

There’s clear evidence that our work has had an impact on student learning. Also, it’s provided a valuable professional learning opportunity for all who participated in the lesson study, including myself. Lewis & Hurd (2011) state that “The real ‘product’ of the lesson study cycle is not the lesson. Lesson study builds educators’ knowledge, motivation, habits of learning, and professional learning community.” (p. 16) We were able to experience this, and it’s the opportunity for this type of learning that keeps me coming back to lesson study.

References

Leinwand et al. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: National Council of Teachers of Mathematics.

Lewis, C & Hurd J. (2011). Lesson study step by step: How teacher learning communities improve instruction. Portsmouth, NH: Heinemann.

Multiplicative Comparison Lesson Study – Part 1

MyLesson

I love lesson study. It provides a structure for slowing down and digging into specific standards and practices, then examining how they affect student learning. This week I was fortunate to have the opportunity to facilitate lesson study with our fourth grade team.

If you’re not familiar with lesson study you can learn more here. Essentially it involves developing a research theme and goals, conducting background research (including formative assessment data), creating and implementing a research lesson, and a post-lesson debrief (driven by data collection during the research lesson). Also, it’s common to revise the research lesson after the first implementation, teach the lesson again, and have a final debrief. Our lesson study schedule was crafted from a timeline embedded within the busy nature of teaching. We carved out a 2 hour after school planning (thanks to strong principal $upport) and a 40 minute PLC. Also, we have a half-day TDE which will allow us to implement the research lesson twice, with a debrief and time to revise in between the two implementations. Altogether, we will have about 6-7 hours for this cycle of lesson study. In my past experiences I’ve always had 12-18 hours, so this is a tight schedule.

The driving question behind our lesson study is, “How do we incorporate what’s working in our intervention block into core instruction?” The idea is that, if we can support students in similar ways during core instruction, we’ll have less students in need of intervening. I selected a few standards that have been challenging this year and presented them to the team. After a little back and forth we settled on CC.4.OA.2 (aka MAFS.4.OA.1.2 in Florida):

Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.

Prior to Meeting

I put together a pre-assessment that would support our study of how students were approaching problems that involve multiplicative comparison. The assessment included three compare problems, each having the unknown in a different position (see Table 2 on p. 89 of the CCSSM document). Each teacher gave the assessment and brought the student work to our first meeting.

The Planning

We took about 15 minutes to orient to lesson study by going over the nuts and bolts of the process, then read chapter 8 of Lesson Study: A Handbook of Teacher-Led Instructional Change by Catherine Lewis which details some common misconceptions of lesson study. Next, we spent some time discussing what it is about the intervention block that is working and came up with this list:

Assessment driven, small group, novelty of a new person, non-routine, exposure, “spiraling” effect, idea of a 2nd chance, research-based resource, differentiated

After this, we dove into the student work, analyzing it item by item. We found that the majority of students could find a solution on the result unknown problems, but struggled with the measurement and partitive division problems that involved comparison. Also, we noticed that a lot of students just took both numbers and multiplied them. Students who were successful typically utilized a number line. We hypothesized that they saw the word “times” and chose to multiply, not really making sense of the problem. Based on this data, we decided to use a partitive division compare problem as the main task of the lesson.

Next, we dug into the available research about comparison problem types. I knew we were time-crunched, so I pulled short chunks of research that would inform us on compare problems and what we may include in the research lesson. We used pg. 29 from K-5 Progression on Counting and Cardinality and Operations and Algebraic Thinking, A short text from Cognitively Guided Instruction on multiplicative comparison problems, and the rubric for Throwing Footballs (a formative assessment task on this standard, complete with detailed rubric). After reading the research, we decided to focus on using visual representations throughout the lesson to support students explanations of problems involving multiplicative comparison.

The Lesson

We embedded opportunities for student discourse about the visuals and the main task throughout the lesson. Here’s the general flow of the lesson:

1) Warm-up – We started by showing students a bar model visual (see below) and prompting with “What do you notice? What do you wonder?” The idea was to use the visual to get students comfortable with the language of multiplicative comparison. This idea came from the first level of the rubric for the Throwing Footballs task.

2) We really liked the football theme with Super Bowl 50 this weekend, so we modified the formative assessment task to be the main task for the lesson:

Two students were trying to see how far they could throw a football. Sadie threw the football 24 yards which was 4 times the distance William threw the football. How many yards did William throw the football?

We anticipated what students would do with the task and planned to focus on encouraging students to make a visual model that matches the problem to encourage sense-making.

3) In the wrap-up (or summary) portion of the lesson we planned on displaying student work, specifically a bar model (or number line) that matches the context of the problem and having students justify which equation (4 x 6 = 24 or 4 x 24) matches the visual model. We planned on addressing 4 x 24 since this is the error we saw most often in the pre-assessment.

What’s Next

This week we will implement the research lesson with two classes. We’ll collect data on what visual models students use and how they’re able to describe problems involving multiplicative comparison. We’re hopeful that the visual representations will support students in making sense of these types of problems. Next week I’ll post a follow-up with samples of student work and how students responded to the research lesson.

The Gift of Questioning

It was 9 years ago when I heard Lucy West say, that in some cultures, a question is viewed as a gift. This has always stuck with me. Since then I’ve been a little obsessed with questioning. Questioning shows up repeatedly in the 8 teaching practices described in Principles to Actions, as well as being one of the practices itself. We know that it takes time for students to adjust to rigorous lines of questioning around mathematical ideas. I’ve seen it firsthand where, upon being asked a question to elicit thinking, a student immediately changes their answer. Then, when probed further, the student changes their answer again. Students often see a question as a subtle way of an adult saying, “You’re wrong.” So, how do we get away from this? I suppose if we asked students these types of questions more often they would adapt. But, how do we model the fielding of tough questions as teachers, and ultimately learners ourselves? Do we embrace them and ponder them? Or, do we immediately try a different answer, then another, until our questioner is appeased? Here are some of the questions that have been gifts for me and students I’ve worked with in the past.

1) Early in my time as an instructional coach I was describing how we were assessing students and tracking their progress to a colleague. He asked me, “So, what are you doing for the students who don’t get it?” I didn’t have an immediate answer for how we were systematically doing this. Discomfort was the immediate effect. But, I allowed the question to sink in, realizing that if I couldn’t answer that, then there was a problem. This question has led to better processes at our school and today we do have an answer for this question. It’s not perfect, but we are using data consistently to identify students who need more help and getting them that help. This question caused immediate discomfort, but was ultimately a gift.

2) About a year ago, I was trying to decide what to do in a situation. Upon asking a colleague for some advice she asked me three questions: How will you feel about your decision in 10 minutes? In 10 days? In 10 years? She didn’t give me an answer to my question, but instead asked me a series of questions that helped me focus on what was important; a real gift.

3) Last year I got to work with a 4th grade class during a formative assessment on multiplicative comparison. The assessment asked students to compare 30 and 300. One student initially compared the two numbers by saying that 300 was 270 more than 30. I asked her to tell me more about how she had figured this out. She explained, but then said, “This isn’t what you’re looking for, is it?” Apparently, I hadn’t brought my poker face A-game. I reassured her that that is one way you can compare two numbers, but asked her, “Could you compare the numbers with multiplication?” Instead of shutting down, she reflected on how she had compared 3 and 12 in the past with multiplication, and applied this to 30 and 300, successfully telling me that 300 was 10 times greater than 30.

I was excited that a few questions bridged the gap between what this student knew and was in the process of learning. I admire the fact that she was able to reflect on the question in the moment without becoming defensive or shutting down. Even though I presented her with a line of questioning that moved her understanding forward, she presented me with a powerful example of staying calm and persevering in the moment of struggle after a challenging question. This is a practice that I hope to aspire to.

My Favorite Thing

As a K-5 math coach, every day I utilize a variety of resources. However, for the last couple of years one continues to come up as my “favorite.” It’s the Mathematics Formative Assessment System (MFAS) which can be found here. The system consists of tasks for each standard and task-specific rubrics. For each level in the rubric there are:

Misconceptions/errors
Examples of student work
Questions to elicit thinking
Instructional implications
Videos of the task being implemented (for some levels of the rubric in some tasks)

The system is coded to the Math Florida Standards which varies slightly from the CCSSM, but it’s fairly easy to transcode, with 1.NBT.2 becoming 1.NBT.2.2 (the cluster is included in the Florida coding). Florida also added on some of there own standards and moved some of the MD domain around a bit (a topic for a completely different post), but rather than that the coding is similar.

So, why is this my favorite thing as of late?

1. It’s free, and it’s research tested. There was a field trial that demonstrated the effects of using the system which you can read about here. It was found that use of the system produced significant results in student learning. It’s not often that you find such a robust resource that’s free of charge.

2. The system blurs the line between instruction and assessment. Someone recently asked, “So, is the system used for instruction or for assessment?” to which I responded, “Yes.” In Principles to Actions, NCTM supports the practice of eliciting and using evidence of student thinking, which essentially blurs the lines between instruction and assessment. The MFAS system supports this practice with tasks that could be used as instructional tasks. The rubrics provides support in the work of anticipating student responses, questions that elicit student thinking, and sequencing the order in which student work could be shared during a class discussion (Smith & Stein, 2011). The tasks could also be administered as a more formal assessment, then used to drive small group differentiated instruction.

3. The system supports a growth mindset. The rubrics typically have 3 stages (Getting Started, Making Progress, Got It) or 4 stages (Getting Started, Moving Forward, Almost There, Got It) based on learning progressions. I love the idea that, at the beginning level of the rubric, you’re “getting started” vs. the idea that you just don’t know it. The language in the system assumes that the student possesses knowledge about the topic that can be used to move them forward. As well as promoting a growth mindset, there’s practical support for how to move students forward. I recently got to hear a 4th grade teacher use this language while differentiating instruction for her class. There was a transparency in the language that supported students’ understanding of where they were, and knowing that they were on their way to mastery of the grade level standard being taught.

This year we have focused heavily on the use of MFAS at my school. Our county has the luxury of a 25 minute math intervention block where we’ve been able to do this work. The exciting thing is that with consistent use we’ve begun to see large groups of students move toward proficiency in the standards. Below are links to some MFAS tasks that I’ve used recently, with correlating standards, if you’d like to check them out:

Kindergarten – Which Set Has One More (K.CC.2.4c)

1st Grade – Use Addition to Solve Subtraction (1.OA.2.4)

2nd Grade – Solving Two-Step Word Problems: Marbles in a Bag (2.OA.1.1)

3rd Grade – Rounding to the Nearest Hundred (3.NBT.1.1)

4th Grade – Seven Hundred Seventy Seven (4.NBT.1.1)

5th Grade – Dividing Using an Area Model With Larger Divisors (5.NBT.2.6)

One Good Thing

Over the past week I was on the lookout for a good thing as part of the MTBoS blogging initiative. I’m a K-5 math coach and this is my third year embedded at the same school. I get to see the folks I work with grow over time. Likewise, they’ve seen me grow over the two and a half years I’ve been there. Early in my time there, there’s no way I could have predicted a week like this past one. It was crazy, possibly one of my busiest of the school year. However, the blogging challenge encouraged me to reflect on where I’m at… currently. Although the week was busy, there were multiple instances where authentic dialogue unfolded about our practice as math educators.

At a math coaches meeting/training this week we had the opportunity to give and receive specific feedback from fellow instructional coaches regarding how we carefully craft coaching conversations.
At a training I facilitated on mathematical discourse a participant hung around after we were “done” to engage in some great conversation around what instructional delivery could look like using a more student-centered approach. I got the opportunity to walk her through a task from the training using John Van de Walle’s before, during, and after model.
While working with a teacher at my school we were able to dialogue around the specifics of how we scaffold students to support productive struggle and the question of how much scaffolding is too much. Also, we both acknowledged that it’s hard work, but didn’t let that stop us from moving forward in exploring this practice.
Multiple teachers sent me emails (without prompting) sharing their assessment data on a current standard. One included students who were proficient, were approaching proficiency, and were not proficient (and the plan for those students moving forward). Exciting!
In multiple planning sessions a grade level team and I were able to work through the math collaboratively using visual models and think through how students will make sense of the tasks for which we were planning.

These are the types of things I envisioned happening when I decided to pursue a role that supports other teachers in the teaching of mathematics. NCTM paints a challenging picture of the principle of professionalism in Principles to Actions, but I feel that this week I got to experience a taste of it in various forms… and that’s a good thing.