Tag Archives: math

Dividing Fractions

Most teachers view the teaching of operations with fractions as challenging. Liping Ma refers to division of fractions as “a topic at the summit of arithemetic.” (1999, p. 55) Lately, I’ve been thinking about the multiplication and division portion of the 4th and 5th grade fraction domains in the Common Core State Standards for Mathematics (CCSSM). Specifically that the standards consistently call for the use of visual models. As a child and a pre-service teacher I wasn’t taught operations with fractions in this way. Because of this I’ve found myself having to work abstract to concrete in order to make sense of what it is students need to know. The funny thing is that the research says we should present learning opportunities that go in the opposite direction, progressing from the concrete to the abstract. In this post I’ll present a few problems that I’ve found in an article about dividing fractions, how I’ve been playing with them, and how they could be revised slightly to support the 5th grade CCSSM.

The first problem from the article:

I eat 2/3 cup of cottage cheese for lunch each day. I have 2 2/3 cups of cottage cheese in my refrigerator. How long will that last me? (Peck and Wood, 2008).

What I like about this problem is that it’s simple and a feasible real life context that surfaces division of fractions. Also, it’s a measurement division context, meaning that we know the groups size and are looking for the amount of groups. So, the problem can be thought of as repeated subtraction. The problem is that it doesn’t meet the 5th grade standard for dividing fractions (MACC.5.NF.2.7) because it’s dividing a mixed number by a fraction. The standard specifies dividing whole numbers by unit fractions and vice versa. So, it could be rewritten as:

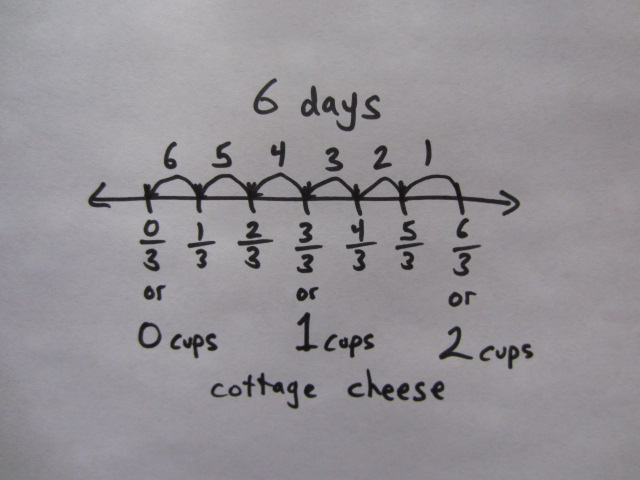
I eat 1/3 cup of cottage cheese for lunch each day. I have 2 cups of cottage cheese in my refrigerator. How long will that last me?

Now, we’re good. This is a task that supports the 5th grade standard. Below are a few representations, including the use of manipulatives, that students could start with before moving on to the equation and trying to generalize a rule for dividing a whole number by a unit fraction. After making sense of the models below, it wouldn’t be a stretch for students to explain why 2 ÷ 1/3 can be solved by inverting the fraction and multiplying, then generalize the rule.

The problem above is a measurement context. What would a partitive problem look like? Let’s take a look at another problem from the article:

I put 2 2/3 gallons of gas into my empty lawn mower. I notice that it is now 2/3 filled. What is the capacity of my gas tank? (Peck and Wood, 2008)

Again, I like the problem, but it doesn’t meet the 5th grade standard. It could be rewritten as:

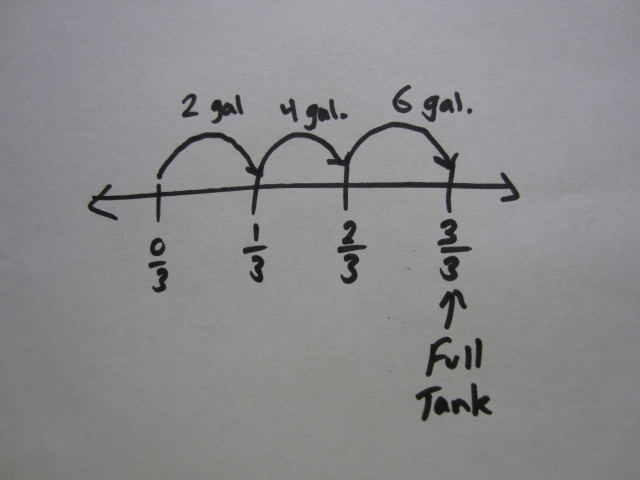
I put 2 gallons of gas into my empty lawn mower. I notice that it is now 1/3 filled. What is the capacity of my gas tank?

Now we have a partitive division problem that supports the 5th grade standard. I still may change the context to cups or ounces because 3 gallons seems like a lot for a lawn mower. Below are a few representations that students could use to solve the problem before explaining and generalizing the rule.

Hopefully this gives you a glimpse into how students can make sense of, explain, and generalize contexts in which they have to divide a whole number by a fraction. Who knows, maybe the new saying will go, “Yours is to reason why we invert and multiply!”

References

Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. New York: Dale Seymour Publications, Educational Development Center.

Peck, S. and Wood, J. (2008). Elastic, cottage cheese, and gasoline: Visualizing division of fractions. Mathematics Teaching in the Middle School. 14(4), 208-212.

Parallels

So, early in the school year I found out that I would be meeting with two reading groups and would have to attend a 2 day Leveled Literacy Intervention (LLI) training. As I was sitting in the training there was a side of me that thought, “Why am I here? I’m a math coach.” I tried to squelch that voice with a positive outlook and look for cross content gems to glean. Sure enough, one of our district reading coaches said something to the effect of, “Running records allow us to get close to students’ reading behaviors.” while giving the rationale for running records being embedded in the LLI routine. I immediately began thinking about what allows teachers to get close to students’ math behaviors. I immediately thought of formative assessments consisting of tasks that are designed to reveal students thinking. How often do we carve out the time to simply sit down and listen to students talk us through their mathematical thinking associated with a task, similar to talking about what they are taking away from a text? How can we meet students where they are if we don’t take the time to do this? The reading research has advocated for making time to listen to student reading for years. Isn’t it time we do the same in mathematics?

Book Review – 5 Practices

One of the challenging aspects of the Common Core State Standards for Mathematics are the SMP’s (Standards for Mathematical Practice). NCTM had similar process standards for years and sometimes I wonder how many people even knew they existed. So, how do we implement the practice standards? How do we ensure that they gain traction in our practice? One way is through math talk which supports various SMP’s, but clearly addresses #3 – construct viable arguments and critique the reasoning of others. For this to occur there has to be communication, which can take many forms, but kids love to talk. The question is how do we plan for purposeful talk? 5 Practices for Orchestrating Productive Mathematics Discussions by Margaret M. Smith and Mary K. Stein is a worthwhile read if you are interested in this topic. The authors present a framework that addresses how to plan for student responses during classroom discussions. The framework includes 5 specific practices: anticipating, sequencing, monitoring, selecting, and connecting. The 5 practices translate directly to a deliberate planning approach that supports more purposeful discussions. At a little over a hundred pages it’s a quick summer read that directly adds to your teaching tools. I strongly recommend this book. You can find the book at NCTM’s website here.

Common Core with Jason Zimba

Jason Zimba and Beth Cocuzza

I was looking forward to this session since I saw that Jason Zimba would be presenting at NCTM this year. He’s one of the lead writers of the Common Core State Standards for Mathematics and I was curious to see what light he would shed on the standards. Zimba and his co-presenter Beth Cocuzza gave a brief history of the CCSSM and how the standards were created. They also highlighted some of the resources available on their site for evaluating CCSSM alignment. My biggest take away was the free resources provided at http://www.achievethecore.net where you can find most of the resources from their session.

Here are my 3 favorite resources from their site:

1) Summary of the shifts (focus, coherence, and rigor). This is helpful for parents, teachers, coaches, and administrators to understand how Common Core is different. The rest of the resources on the site typically connect back to one of the three shifts. Zimba explained that the focus of the standards gives the space for the eight mathematical practice standards to be addressed. This made a lot of sense. He also explained that the coherence across grade levels meant that each year students should be adding on to their current understanding of topics rather than seeing ideas as brand new. The summary of the shifts can be found here.

2) Practicing with the Shifts handout provides exercises for better understanding each shift. In the focus exercise you are asked to narrow down the focus of grades K-8 by eliminating 1 out of 3 provided topics for each grade level. There’s an answer key provided here. In the coherence exercise you essentially go on a “standards hunt” to find all the standards that relate to a topic across grade levels. Fractions is the specified topic in the exercise, but I could see this being done with any topic: addition, geometry, measurement, etc. This is a valuable exercise in collaborative teams (or across grade levels) to get familiar with the coherence within and across grade levels. There’s also a section where you’re able to explore what’s meant by rigor in the CCSSM. The practice handout can be found here.

3) Focus by Grade Level documents. These documents provide a 2 page synopsis of individual grade levels. Each document defines the major, supporting, and additional clusters (of standards) for the grade level. It’s recommended that 65 to 85 percent of time be spent on the major clusters at each grade level. Also, the required fluencies for each grade level are highlighted. The back shows the clusters of standards that lead to 8th grade algebra. I really like these documents because they give a brief, but concise snapshot of each grade level and also inform teachers where their instruction fits within the big picture of the standards. The Focus by Grade Level documents can be found here.

Overall, the presentation was very informative. It didn’t get into the day to day details of what the standards look like in practice, but provided some excellent resources for anyone looking to better their understanding of the structure and purpose of the standards. Also, there are many other resources available at http://www.achievethecore.net.

It’s Been a While…

The annual NCTM conference starts tomorrow and I’m excited to attend this year. The last time I was able to attend the conference was in 2003 in San Antonio, TX. This was also my first year teaching. I remember feeling honored to have the opportunity to attend as a first year teacher and it really set the stage for my passion for teaching mathematics. I’m really looking forward to this year’s conference, especially with the shifts associated with Common Core. I’ll be recapping some of the sessions I attend and sharing as much info as possible in my posts. A couple that I’m really looking forward to are:

“Key Words Help,” “Inquiry Won’t Work,” and Other Myths (Speakers: Alexis Dixon and Juli Dixon)

Evaluating Alignment to CCSSM: How Do Your Resources Rate? (Speakers: Beth Cocuzza and Jason Zimba)